编程学习

代码速查专用文。

numpy

统计分析与数据拟合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt

# 生成带噪声的数据
x = np.linspace(0, 10, 100)
noise = np.random.normal(0, 0.5, 100)
y = 2*x + 1 + noise

# 多项式拟合
coeffs = np.polyfit(x, y, 1)  # 1次多项式（线性）拟合
poly = np.poly1d(coeffs)
print("拟合结果: y =", poly)

# 计算相关系数
correlation = np.corrcoef(x, y)[0, 1]
print("相关系数:", correlation)

# 数据统计
mean = np.mean(y)
median = np.median(y)
std_dev = np.std(y)
print(f"均值: {mean}, 中位数: {median}, 标准差: {std_dev}")

# 可视化拟合结果
plt.scatter(x, y, label='原始数据')
plt.plot(x, poly(x), 'r-', label='拟合曲线')
plt.legend()
plt.show()

常见的函数

数组创建

函数 功能描述
np.array() 从列表或元组创建数组
np.zeros() 创建全0数组
np.ones() 创建全1数组
np.empty() 创建未初始化的数组
np.arange() 创建等差数列数组
np.linspace() 创建指定间隔内的等分点数组
np.eye() 创建单位矩阵
np.random.rand() 创建[0,1)均匀分布随机数数组
np.random.randn() 创建标准正态分布随机数数组

随机数生成

函数 功能描述
np.random.seed() 设置随机数种子
np.random.shuffle() 随机打乱数组
np.random.choice() 从给定数组中随机选择
np.random.normal() 生成正态分布随机数
np.random.uniform() 生成均匀分布随机数

数学运算

函数 功能描述
np.add() 元素级加法
np.subtract() 元素级减法
np.multiply() 元素级乘法
np.divide() 元素级除法
np.power() 元素级幂运算
np.sqrt() 元素级平方根
np.sin(), np.cos() 三角函数
np.exp(), np.log() 指数和对数函数
np.sum() 求和
np.mean() 求平均值
np.std() 求标准差
np.var() 求方差
np.min(), np.max() 求最小/最大值
np.argmin(), np.argmax() 求最小/最大值的索引

排序和搜索

函数 功能描述
np.sort() 排序数组
np.argsort() 返回排序后的索引
np.searchsorted() 在排序数组中查找插入点

线性代数

函数 功能描述
np.dot() 点积/矩阵乘法
np.matmul() / @ 矩阵乘法
np.linalg.inv() 求逆矩阵
np.linalg.det() 求行列式
np.linalg.eig() 求特征值和特征向量
np.linalg.svd() 奇异值分解
np.linalg.norm() 求范数
np.linalg.solve() 求解线性方程组

蒙特卡洛模拟

1
2
3
4
5
6
7
# 蒙特卡洛积分计算π
def monte_carlo_pi(n):
    points = np.random.rand(n, 2)  # 生成n个[0,1)x[0,1)的随机点
    inside_circle = np.sum(np.sum(points**2, axis=1) < 1)  # 计算在单位圆内的点数
    return 4 * inside_circle / n  # π的估计值

print(f"π的蒙特卡洛估计值: {monte_carlo_pi(100000)}")

信号处理与傅里叶变换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#生成信号
t = np.linspace(0, 1, 1000)
f1, f2 = 5, 20  # 5Hz和20Hz的信号
signal = np.sin(2*np.pi*f1*t) + 0.5*np.sin(2*np.pi*f2*t)

# 执行傅里叶变换
fft_result = np.fft.fft(signal)
freqs = np.fft.fftfreq(len(t), t[1]-t[0])

# 计算功率谱
power = np.abs(fft_result)**2

# 绘制原始信号和频谱
plt.figure(figsize=(12, 6))
plt.subplot(211)
plt.plot(t, signal)
plt.title('时域信号')
plt.xlabel('时间 (s)')

plt.subplot(212)
plt.plot(freqs[:len(freqs)//2], power[:len(freqs)//2])
plt.title('频谱')
plt.xlabel('频率 (Hz)')
plt.tight_layout()
plt.show()

pandas

读入数据csv/xlsx

1
2
3
4
5
6
7
8
9
#加载数据
# 从CSV文件加载
df = pd.read_csv('data.csv')  # 假设存在这个文件
# 或创建示例数据
data = {
    'x': np.linspace(0, 10, 100),
    'y': 2 * np.linspace(0, 10, 100) + np.random.normal(0, 1, 100)
}
df = pd.DataFrame(data)

写出数据csv/xlsx

1
df.to_excel("result1.xlsx")

表格设置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd

# 使用字典创建 DataFrame 时设置列名
df = pd.DataFrame({
    'A列': [1, 2, 3],
    'B列': [4, 5, 6],
    'C列': [7, 8, 9]
}, index=['第一行', '第二行', '第三行'])  # 设置行名(索引)

# 使用嵌套列表创建
data = [[1, 4, 7], [2, 5, 8], [3, 6, 9]] #data本身是嵌套的list
df = pd.DataFrame(data, 
                  index=['第一行', '第二行', '第三行'])  # 设置行名
				  columns=['A列', 'B列', 'C列'],  # 设置列名
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#一个更加科学的设置方式
num_time_steps = 301
num_nodes = 223

data = [[0]*num_time_steps for _ in range(2*num_nodes)]

row_names =[]
for i in range(num_nodes):
	row_names.append(f"Node_{i}_x")
	row_names.append(f"Node_{i}_y")

col_names = list(range(num_time_steps))
df=pd.DataFrame(data, index=row_names, columns=col_names)
df.to_excel("result1.xlsx")

数据清洗

数据清洗是数据分析流程中的关键步骤。pandas 提供了丰富的工具来处理各种数据问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 读取数据
df = pd.read_csv('messy_data.csv')

# 1. 数据概览
# 查看前几行数据df.head()
# 数据基本信息df.info()
# 统计摘要df.describe()
# 检查缺失值df.isnull().sum()
# 检查数据类型df.dtypes

print("数据基本信息:")
print(df.info())
print("\n缺失值统计:")
print(df.isnull().sum())

# 2. 数据类型转换
df['date'] = pd.to_datetime(df['date'], errors='coerce')
df['income'] = pd.to_numeric(df['income'], errors='coerce')

# 3. 处理缺失值
# 删除包含缺失值的行df_cleaned = df.dropna()
# 删除特定列中有缺失值的行df_cleaned = df.dropna(subset=['column_name'])
# 填充缺失值为指定值df['column_name'].fillna(0, inplace=True)
# 使用均值填充数值型缺失值df['numeric_column'].fillna(df['numeric_column'].mean(), inplace=True)
# 使用中位数填充df['numeric_column'].fillna(df['numeric_column'].median(), inplace=True)
# 使用众数填充分类变量df['category_column'].fillna(df['category_column'].mode()[0], inplace=True)
# 使用前向填充df['column_name'].fillna(method='ffill', inplace=True)
# 使用后向填充df['column_name'].fillna(method='bfill', inplace=True)
# 插值填充df['numeric_column'].interpolate(method='linear', inplace=True)

# 日期使用前值填充
df['date'].fillna(method='ffill', inplace=True)
# 收入使用中位数填充
df['income'].fillna(df['income'].median(), inplace=True)
# 类别使用众数填充
df['category'].fillna(df['category'].mode()[0], inplace=True)

# 4. 去除重复值
df.drop_duplicates(inplace=True)

# 5. 处理异常值
# 使用IQR方法处理income中的异常值
Q1 = df['income'].quantile(0.25)
Q3 = df['income'].quantile(0.75)
IQR = Q3 - Q1
df = df[~((df['income'] < (Q1 - 1.5 * IQR)) | (df['income'] > (Q3 + 1.5 * IQR)))]

# 6. 标准化数值特征
df['income_std'] = (df['income'] - df['income'].mean()) / df['income'].std()

# 7. 处理文本数据
df['notes'] = df['notes'].str.strip().str.lower()

# 8. 创建新特征
df['year'] = df['date'].dt.year
df['month'] = df['date'].dt.month

# 9. 对分类变量进行编码
df_encoded = pd.get_dummies(df, columns=['category'])

# 10. 最终检查
print("\n清洗后的数据信息:")
print(df_encoded.info())
print("\n清洗后的样本数据:")
print(df_encoded.head())

# 11. 保存清洗后的数据
df_encoded.to_csv('cleaned_data.csv', index=False)

matplotlib.pyplot

绘图代码

1
2
3
4
5
6
7
8
9
10
def draw():
    n=16
    theta=np.linspace(0, 2*n*np.pi,1000)
    r=a+b*theta

    x=r*np.cos(theta)
    y=r*np.sin(theta)
    plt.figure(figsize=(8,8))
    plt.plot(x, y)
    plt.show()

解各类方程

fsolve()函数

SciPy``` 优化模块 ```scipy.optimize``` 中的一个函数，用于求解非线性方程组的**根（零点）**。它是数值分析中常用的函数求根工具。
1
2
3
4

```python
#基本语法
scipy.optimize.fsolve(func, x0, args=())
  1. func：要求解的函数
    • 函数必须接受一个向量作为第一个参数，返回一个数组或向量
    • 当函数返回值为0时，对应的输入即为方程的根
  2. x0：初始猜测值
    • 求解过程的起点，类型为标量或数组
    • 好的初始猜测可以大大提高求解效率和成功率
  3. args：额外参数
    • 以元组形式传递给函数的附加参数
    • args=(t,)是将时间 t作为附加参数传递给 func函数

返回值

  • 默认返回找到的根 x
  • 如果full_output=True，则返回元组(x, infodict, ier, mesg)：
    • x：根的最终估计值
    • infodict：包含收敛信息的字典
    • ier：整数标志，指示是否成功收敛
    • mesg：详细信息字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#插值，做反函数，求出初始猜测值
from scipy.optimize import fsolve
from scipy.interpolate import interp1d

def inverse(t):
    def F(theta):
        def func(theta):
            return b * (0.5*theta*np.sqrt(1+theta**2) + 0.5*np.log(theta + np.sqrt(1+theta**2)))
        return func(32*np.pi)-func(theta)
    theta_val=np.linspace(0, 32*np.pi,1000)
    F_val = F(theta_val)#样本点
    F_inv_approx = interp1d (F_val,theta_val,kind='linear',fill_value='extrapolate')
    theta0=F_inv_approx(v0*t)
    return theta0

def get_theta1(t):
    theta0 = inverse(t)
    solution =fsolve(integral_equation, x0=theta0, args=(t,)) 
    # 因为这是一个完全单调递增的函数，所以可以使用fsolve如果是特殊类型的、有多解的函数不可以这样！！！可以试着用二分查找
    theta1 = solution[0] #结果是一个向量，要取第一位
    print(f"解得 theta1 = {theta1}")
    return theta1

实际使用建议

  1. 提供一个好的初始猜测值（如反函数插值得到的值）
  2. 检查返回值确保收敛（可使用 full_output=True）
  3. 对于困难问题，考虑提供函数导数或使用其他求解器
  4. 对多解问题，**不可直接套用！！！！**尝试使用其他优化方法（如二分法）

interp1d ()函数——插值拟合

```SciPy ```插值模块 ```scipy.interpolate``` 中的一个重要函数，用于一维插值。它基于已知数据点创建一个插值函数，能够估计任意中间点的值。
1
2
3
4
5
6
7
8
9
10
11
12

**基本功能**

```interp1d```构建一个函数，用于近似两组数据点之间的关系：

- 给定一组 x 值和对应的 y 值
- 返回一个可调用对象，用于预测新 x 值对应的 y 值

```python
#基本语法
scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, 
                          bounds_error=True, fill_value=nan, assume_sorted=False)
  1. x: 自变量数据点（必须是递增或递减的）
  2. y: 因变量数据点（与 x 长度相同）
  3. kind: 插值方法类型
    • 'linear': 线性插值（默认）
    • 'cubic': 三次样条插值
    • 'quadratic': 二次样条插值
    • 'nearest': 最近邻插值
    • 整数 k: k 阶样条插值
  4. fill_value: 当bounds_error=False时，为范围外点指定的值
    • 可以是单个值或一对值 (下边界值, 上边界值)
    • 'extrapolate': 允许基于最近两个点的插值方法进行外推
1
2
3
4
5
6
7
8
9
10
11
#example:实现了一个反函数
def inverse(t):
    def F(theta):
        def func(theta):
            return b * (0.5*theta*np.sqrt(1+theta**2) + 0.5*np.log(theta + np.sqrt(1+theta**2)))
        return func(32*np.pi)-func(theta)
    theta_val=np.linspace(0, 32*np.pi,1000)
    F_val = F(theta_val)  # 样本点
    F_inv_approx = interp1d(F_val, theta_val, kind='linear', fill_value='extrapolate')
    theta0 = F_inv_approx(v0*t)
    return theta0

sympy库与常微分方程

基础操作

函数/对象 功能描述
symbols() 创建符号变量
Symbol() 创建单个符号
var() 创建并注入符号到命名空间
sympify() 将字符串或数字转换为 SymPy 表达式
lambdify() 将 SymPy 表达式转换为可调用函数
N() 数值评估表达式
simplify() 表达式简化
expand() 展开表达式
factor() 因式分解
collect() 合并同类项

微积分

函数/对象 功能描述
diff() 求导数
Derivative() 创建导数对象
integrate() 求积分
Integral() 创建积分对象
limit() 求极限
series() 计算级数展开
summation() 求和

代数与方程

函数/对象 功能描述
solve() 解方程和方程组
solveset() 新的解方程接口，返回集合
linsolve() 解线性方程组
nonlinsolve() 解非线性方程组
Eq() 创建等式
roots() 求多项式方程的根
apart() 部分分式分解
together() 合并分母
cancel() 约分

微分方程

函数/对象 功能描述
dsolve() 解常微分方程
pdsolve() 解偏微分方程
ode_order() 确定ODE的阶数
checkodesol() 验证ODE解的正确性
classify_ode() 分类常微分方程 
1
2
import sympy as sp

偏微分方程

1

优化算法

模拟退火算法Simulated Annealing(SA)

一文读懂模拟退火算法：从原理到实战

模拟退火算法是一种启发式算法，用于在解空间中寻找问题的全局最优解。它模拟物体在高温状态下的退火过程，通过接受可能使目标函数增加的解，有助于跳出局部最优解，最终找到全局最优解。

模拟退火算法的核心思想是通过在解空间中接受可能不是全局最优解的解，以一定的概率接受较差的解，逐步降低接受较差解的概率，从而在整个解空间中搜索到全局最优解。

模拟退火算法的成功与否很大程度上取决于温度的调度策略。温度的降低速率应该足够慢，以确保算法有足够的时间跳出局部最优解。

主要用于解决：NP完全问题，如旅行商问题(Travelling Salesman Problem，简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为e(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

模拟退火算法在全局最优性方面具有较好的表现，尤其适用于处理复杂、非凸的最优化问题。与梯度下降算法相比，模拟退火算法能够避免陷入局部最优，而遗传算法则具有更强的全局搜索能力，适用于更复杂的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

`dual_annealing` 返回一个 `OptimizeResult` 对象，其中包含：

- `x`: 最优解向量
- `fun`: 最优解处的函数值
- `nfev`: 函数评估次数
- `nit`: 迭代次数
- `success`: 是否成功找到解
- `message`: 描述终止原因的消息

```python
from scipy import optimize
import numpy as np

# 定义目标函数
def objective_function(x):
    return x[0]**2 + x[1]**2  # 例如：最小化 f(x,y) = x² + y²

# 定义初始解
initial_state = [5.0, 5.0]

# 调用模拟退火算法
result = optimize.dual_annealing(
    objective_function,
    bounds=[(-10, 10), (-10, 10)],  # 各变量的取值范围
    maxiter=1000,                    # 最大迭代次数
    initial_temp=5230,               # 初始温度
    restart_temp_ratio=2e-5,         # 重启温度比率
    visit=2.62,                      # 访问参数
    accept=-5.0,                     # 接受参数
    no_local_search=False            # 是否执行局部搜索
)

print("最优解: x =", result.x)
print("最优值: f(x) =", result.fun)

使用模拟退火算法解决TSP问题的一个实例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import numpy as np
from scipy.optimize import dual_annealing
import matplotlib.pyplot as plt

# 计算城市间距离
def distance(city1, city2):
    return np.sqrt(np.sum((city1 - city2) ** 2)) #或者用np.linalg.norm(city1-city2)

# 总路程计算函数（作为优化目标）
def objective_function(x, cities):
    # 将连续变量转换为排列
    path = np.argsort(x) #返回排序后的索引
    
    # 计算路径总长度
    dist = 0
    for i in range(len(path) - 1):
        dist += distance(cities[path[i]], cities[path[i + 1]])
    dist += distance(cities[path[-1]], cities[path[0]])  # 返回起点
    
    return dist

def solve_tsp_with_dual_annealing(cities):
    n_cities = len(cities)
    
    # 设置初始猜测和边界（对应每个城市的排序值）
    x0 = np.random.rand(n_cities)
    bounds = [(0, 1)] * n_cities
    
    # 运行优化
    result = dual_annealing(
        objective_function, 
        bounds=bounds, 
        args=(cities,),
        maxiter=1000,
        initial_temp=100,
        restart_temp_ratio=2e-5,
        visit=2.0,
        no_local_search=False
    )
    
    # 获取最优解
    best_path = np.argsort(result.x)
    best_distance = result.fun
    
    return best_path, best_distance

# 可视化结果
def plot_tsp_solution(cities, path):
    plt.figure(figsize=(10, 6))
    
    # 绘制城市点
    plt.scatter(cities[:, 0], cities[:, 1], c='red', s=100)
    
    # 添加城市标签
    for i, city in enumerate(cities):
        plt.annotate(f"City {i}", (city[0], city[1]), xytext=(10, 10), 
                    textcoords='offset points')
    
    # 绘制路径
    path_with_return = np.append(path, path[0])  # 添加回起点
    plt.plot(cities[path_with_return, 0], cities[path_with_return, 1], 'b-')
    
    plt.title("TSP Solution")
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.grid(True)
    plt.show()

# 测试
if __name__ == "__main__":
    # 城市坐标
    cities = np.array([[0, 0], [1, 3], [2, 5], [3, 2], [4, 6]])
    
    # 解决TSP
    best_path, best_distance = solve_tsp_with_dual_annealing(cities)
    
    print("Best path:", best_path)
    print("Best distance:", best_distance)
    
    # 可视化
    plot_tsp_solution(cities, best_path)

遗传算法Genetic Algorithm (GA)

干货 | 遗传算法(Genetic Algorithm) （附代码及注释）

遗传算法是一种模拟生物自然进化过程的优化算法，核心思想来自“适者生存、基因重组、基因突变“的生物进化理论。它就像一场“解的进化比赛”：一群候选解（种群）通过“竞争”（选择）、“学习”（交叉）、“创新”（变异），逐步淘汰差的解，保留并优化好的解，最终找到复杂问题的最优解（如函数最大值、旅行商最短路径、背包问题最优解等）。

遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。

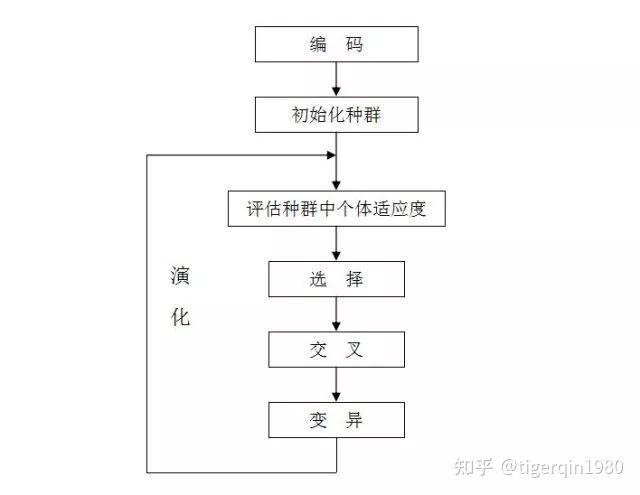
遗传算法的执行过程：

遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。

染色体作为遗传物质的主要载体，即多个基因的集合，**其内部表现（即基因型）是某种基因组合，**它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。**因此，在一开始需要实现从表现型到基因型的映射即编码工作。**由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。

初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

使用PyGAD库来调用遗传算法：

基本参数

参数 类型 说明 默认值
num_generations 整数 进化代数 100
num_parents_mating 整数 用于生成后代的父代数量 取决于种群大小
sol_per_pop 整数 种群大小 100
num_genes 整数 每个个体的基因数量 必须指定
gene_type 数据类型 基因类型(int, float等) float
gene_space 列表/范围 基因可能的取值范围 None
fitness_func 函数 适应度函数 必须指定

遗传算子参数

参数 类型 说明 默认值
initial_population 数组 初始种群 None (随机生成)
parent_selection_type 字符串 父代选择方式 “sss” (稳态选择)
crossover_type 字符串 交叉操作类型 “single_point”
crossover_probability 浮点数 交叉概率 None
mutation_type 字符串 变异类型 “random”
mutation_probability 浮点数 变异概率 None
mutation_percent_genes 整数/浮点数 变异基因百分比 10%

进阶参数

参数 类型 说明 默认值
keep_parents 整数/字符串 保留父代数量 -1 (全部保留)
keep_elitism 整数 精英数量 1
K_tournament 整数 锦标赛选择参数 3
stop_criteria 字符串/列表 停止条件 None
delay_after_gen 浮点数 每代后延迟时间 0.0
save_best_solutions 布尔值 是否保存最优解 False
save_solutions 布尔值 是否保存所有解 False
suppress_warnings 布尔值 是否抑制警告 False

选择、交叉和变异操作详解

父代选择方式 parent_selection_type

  • "sss" (Steady-State Selection): 稳态选择
  • "rws" (Roulette Wheel Selection): 轮盘赌选择
  • "sus" (Stochastic Universal Selection): 随机通用采样
  • "rank": 排名选择
  • "random": 随机选择
  • "tournament": 锦标赛选择

交叉类型 crossover_type

  • "single_point": 单点交叉
  • "two_points": 两点交叉
  • "uniform": 均匀交叉
  • "scattered": 分散交叉

变异类型 mutation_type

  • "random": 随机变异
  • "swap": 交换变异
  • "inversion": 反转变异
  • "scramble": 扰乱变异
  • "adaptive": 自适应变异
1
2
#example：解决TSP问题

蚁群算法Ant Colony Optimization (ACO)

1

K-means聚类算法

1

元胞自动机

深度学习